【题解】AT_dp_z Frog 3

Pre

题目链接。

这才是属于斜率优化的模板题，转移方程简单，公式转化也简单。

Statement

有 $N$ 个石头，编号为 $1,2,\dots,N$，第 $i$ 个高为 $h_i$。保证 $h$ 严格单调递增。

有一只青蛙在第一个石头上，它可以跳到石头编号为 $i + 1, i + 2, \dots, N$。当他跳到编号 $j$ 石头时的花费是
$(h_i - h_j) ^ 2 + C$。求跳到编号为 $N$ 石头的最小花费。

Solution

Transform

首先转移方程可以直接秒掉，定义 $dp_i$ 表示落到第 $i$ 个石头上的最小代价，有：

$$dp_i = \min_{j < i} dp_j + (h_i - h_j) ^ 2 + C$$

然后参数分离，有：

$$\begin{aligned} dp_i &= \min_{j < i} (dp_j + h_i ^ 2 - 2h_ih_j + h_j ^ 2 + C) \\ &= h_i ^ 2 + C + \min_{j < i} (dp_j + h_j ^ 2 - 2h_ih_j) \end{aligned}$$

令 $k \gets -2h_i$，$F_i \gets dp_i + h_i ^ 2$，则有

$$dp_i = 2 + C + \min_{j < i} (F_j + k \times h_j)$$

考虑枚举 $j(j \lt i)$，不妨设 $j_1,j_2$ ($j_1 \lt j_2 \lt i$) 并且 $j_1$ 不劣于 $j_2$，则有不等式：

$$\begin{aligned} F_{j_1} + k \times h_{j_1} &\le F_{j_2} + k \times h_{j_2} \\ k \times (h_{j_1} - h_{j_2}) &\le F_{j_2} - F_{j_1} \\ \end{aligned}$$

由于 k 为负数，移项后则有：

$$\begin{aligned} -2 h_i &\le \frac{F_{j_2} - F_{j_1}}{h_{j_1} - h_{j_2}} \\ \frac{F_{j_1} - F_{j_2}}{h_{j_1} - h_{j_2}} &\ge 2h_i \end{aligned}$$

至此，斜率就求出来了，斜率求最接近 $2h_i$ 的即可，解释如下。

Simulation

定义 $slope(i, j)$ 表示 $i,j$ 两点的斜率，实现函数如下（与公式相关联）：

1
2
3

inline double X(int i) { return (double)f[i] + (double)h[i] * h[i]; }
inline double Y(int i) { return (double)h[i]; }
inline double slope(int i, int j) { return (X(i) - X(j)) / (Y(i) - Y(j)); }

若有三个点 $i,j,k\ (i \lt j \lt \ k)$，并且最优的决策点为 $j$，根据上述公式，有：

$$slope(i, j) \le 2 h_i \\ slope(j, k) \ge 2 h_i \\ \Rightarrow slope(i, j) \le 2 h_i \le slope(j, k)$$

由此可知每个 $slope$ 的值应当尽可能的小，然后就维护出来一个凸包：

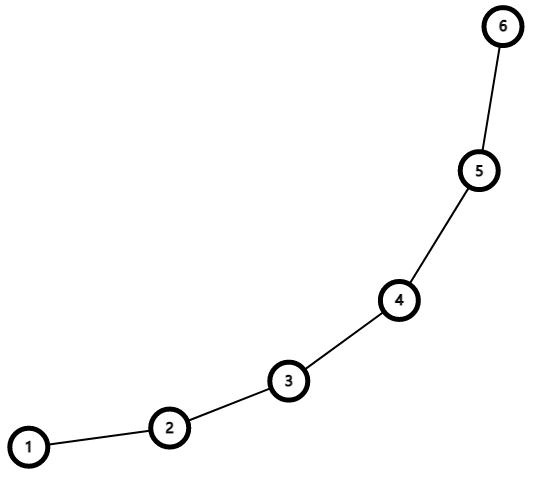
处理出来了二分即可，但是本题很显然是单调的，因此使用单调队列即可，注意到不像一般的队列一样，队列当中应当至少有一个元素，因为至少三个元素才可以进项比较。

Code

1
2
3
4
5
6
7
8
9

que[++ tt] = 1;
for (int i = 2; i <= n; i ++)
{
    while (hh < tt && slope(que[hh], que[hh + 1]) <= 2.0 * h[i]) hh ++;
    f[i] = f[que[hh]] + (h[i] - h[que[hh]]) * (h[i] - h[que[hh]]) + C;
    while (hh < tt && slope(que[tt - 1], que[tt]) >= slope(que[tt], i)) tt --;
    que[++ tt] = i;
}
cout << f[n] << '\n';