前言
这一节用于讲解拉格朗日插值法(Lagrange Polynomial)和快速傅里叶变换(Fast Fourier Transform),但是含有前置知识,因此有大量学过的知识可以直接跳过,存在大量证明会放出相应的链接。
多项式
基本概念
我们将形如 ∑ a n x n \textstyle{\sum a_nx^n} ∑ a n x n 有限项相加 式子成为多项式 ,记作 f ( x ) = ∑ i = 0 n a i x i f(x) = \textstyle{\sum_{i = 0}^n a_i x^i} f ( x ) = ∑ i = 0 n a i x i
如果是形如 ∑ i = 0 ∞ a i x i \textstyle{\sum_{i = 0}^\infty a_i x^i} ∑ i = 0 ∞ a i x i 无限项相加 式,则称为形式幂级数 ,后面应该会讲到。
a i a_i a i i i i 系数 ,记作 [ x i ] f ( x ) : = a i [x ^ i]f(x) := a_i [ x i ] f ( x ) := a i ∀ a i ( i > n ) \forall a_i(i \gt n) ∀ a i ( i > n ) 0 0 0
多项式的系数非零的最高次项的次数 为该多项式的度 ,也为该多项式的次数,记作 deg f \deg f deg f
使得 f ( x ) = 0 f(x) = 0 f ( x ) = 0 x x x 根 。
如果 ∀ a i ( 0 < i ≤ n ) , a i ∈ R \forall a_i(0 \lt i \le n), a_i \in \mathbb{R} ∀ a i ( 0 < i ≤ n ) , a i ∈ R f f f
以上都是初中知识范畴里的,可以直接跳过。
代数基本定理
任何非零一元 n n n n n n 可重合复数根 。
证明有兴趣详见代数基本定理的证明 ,证明需要的知识不在我们学习之内。但是这个定理对于后面的多项式插值以及像 FFT 等变换很重要的推动作用。
多项式的两种表示方法
第一种也是最常见的一种方法:系数表示法 。这种方式直接表示出了多项式 f ( x ) f(x) f ( x )
第二种同样十分重要:点值表示法 。我们选取多个不同的 x i x_i x i x i x_i x i f ( x ) f(x) f ( x ) ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , … (x_0, y_0), (x_1, y_1), (x_2, y_2), \dots ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , … x i x_i x i f f f
至于如何确定,这就相当于解一个 n n n
先给出结论:n n n n − 1 n - 1 n − 1
一个感性的理解是:n − 1 n - 1 n − 1 n n n n n n n − 1 n - 1 n − 1
详细的证明采用范德蒙德矩阵 ,具体地:对于任意 0 ≤ j < n , ∑ i = 0 n − 1 a i x j i = y j 0 \le j \lt n, \textstyle{\sum_{i = 0}^{n - 1} a_ix_j^i = y_j} 0 ≤ j < n , ∑ i = 0 n − 1 a i x j i = y j
[ 1 x 0 x 0 2 ⋯ x 0 n − 1 1 x 1 x 1 2 ⋯ x 1 n − 1 1 x 2 x 2 2 ⋯ x 2 n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n − 1 x n − 1 2 ⋯ x n − 1 n − 1 ] \begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\
1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\
1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1}
\end{bmatrix}
1 1 1 ⋮ 1 x 0 x 1 x 2 ⋮ x n − 1 x 0 2 x 1 2 x 2 2 ⋮ x n − 1 2 ⋯ ⋯ ⋯ ⋱ ⋯ x 0 n − 1 x 1 n − 1 x 2 n − 1 ⋮ x n − 1 n − 1
其中 x i x_i x i 范德蒙德矩阵的性质 ,矩阵行列式不为 0 0 0 n n n n n n
这两种表示法显然可以互相转换,我们把从系数表示法转换为点值表示法的过程称为求值 (Evaluation )。
相反地,我们把逆过程成为插值 (Interpolation )。
基本运算
系数表示法下,设两个多项式 f ( x ) = ∑ i = 0 n a i x i f(x) = \textstyle{\sum_{i = 0} ^ n a_i x^i} f ( x ) = ∑ i = 0 n a i x i g ( x ) = ∑ i = 0 m b i x i g(x) = \textstyle{\sum_{i = 0} ^ m b_i x^i} g ( x ) = ∑ i = 0 m b i x i n n n m m m
多项式之间可以进行加法,定义 h : = f + g = ∑ i = 0 n a i x i + ∑ i = 0 m b i x i h := f + g = \textstyle{\sum_{i = 0} ^ n a_i x^i} + \textstyle{\sum_{i = 0} ^ m b_i x^i} h := f + g = ∑ i = 0 n a i x i + ∑ i = 0 m b i x i
h = ∑ i = 0 max ( n , m ) ( a i + b i ) x i h = \sum_{i = 0}^{\max(n, m)} (a_i + b_i) x^ i
h = i = 0 ∑ m a x ( n , m ) ( a i + b i ) x i
可以得到 deg h = deg ( f + g ) = max ( deg f , deg g ) \deg h = \deg (f + g) = \max(\deg f, \deg g) deg h = deg ( f + g ) = max ( deg f , deg g )
多项式之间可以进行乘法,定义 h : = f ⋅ g = ( ∑ i = 0 n a i x i ) × ( ∑ i = 0 m b i x i ) h := f \cdot g = (\textstyle{\sum_{i = 0} ^ n a_i x^i}) \times (\textstyle{\sum_{i = 0} ^ m b_i x^i}) h := f ⋅ g = ( ∑ i = 0 n a i x i ) × ( ∑ i = 0 m b i x i )
h = ∑ i = 0 n + m ( ∑ j = 0 i a j b i − j ) x i h = \sum_{i = 0}^{n + m} \left ( \sum_{j = 0}^i a_j b_{i - j}\right ) x^i
h = i = 0 ∑ n + m ( j = 0 ∑ i a j b i − j ) x i
可以得到 deg h = d e g ( f ⋅ g ) = deg f + deg g \deg h = deg(f \cdot g) = \deg f + \deg g deg h = d e g ( f ⋅ g ) = deg f + deg g
因此在系数表示法下,我们可以在 O ( max ( n , m ) ) \mathcal{O}(\max(n, m)) O ( max ( n , m )) O ( m n ) \mathcal{O}(mn) O ( mn )
点值表示法下,设 f ( x ) : ( x 0 , y 0 ) , ( x 1 , y 1 ) , … , ( x n , y n ) f(x):(x_0, y_0), (x_1, y_1),\dots,(x_n, y_n) f ( x ) : ( x 0 , y 0 ) , ( x 1 , y 1 ) , … , ( x n , y n ) g ( x ) : ( x 0 , y 0 ′ ) , ( x 1 , y 1 ′ ) , … , ( x m , y m ′ ) g(x):(x_0, y_0'), (x_1, y_1'),\dots,(x_m, y_m') g ( x ) : ( x 0 , y 0 ′ ) , ( x 1 , y 1 ′ ) , … , ( x m , y m ′ ) n , m ( n ≤ m ) n,m(n \le m) n , m ( n ≤ m )
它们之间进行加法,h ( x ) : = f ( x ) + g ( x ) = ( f + g ) ( x ) h(x) := f(x) + g(x) = (f + g)(x) h ( x ) := f ( x ) + g ( x ) = ( f + g ) ( x )
h ( x ) : ( x 0 , y 0 + y 0 ′ ) , ( x 1 , y 1 + y 1 ′ ) , … , ( x n , y n + y n ′ ) , … , ( x m , y m + y m ′ ) h(x):(x_0, y_0 + y_0'), (x_1, y_1 + y_1'),\dots,(x_n, y_n + y_n'),\dots,(x_m, y_m + y_m')
h ( x ) : ( x 0 , y 0 + y 0 ′ ) , ( x 1 , y 1 + y 1 ′ ) , … , ( x n , y n + y n ′ ) , … , ( x m , y m + y m ′ )
它们之间进行乘法,h ( x ) : = f ( x ) g ( x ) = ( f g ) ( x ) h(x) := f(x)g(x) = (fg)(x) h ( x ) := f ( x ) g ( x ) = ( f g ) ( x )
h ( x ) : ( x 0 , y 0 y 0 ′ ) , ( x 1 , y 1 y 1 ′ ) , … , ( x n , y n y n ′ ) , … , ( x m , y m y m ′ ) h(x):(x_0, y_0 y_0'), (x_1, y_1 y_1'),\dots,(x_n, y_n y_n'),\dots,(x_m, y_m y_m')
h ( x ) : ( x 0 , y 0 y 0 ′ ) , ( x 1 , y 1 y 1 ′ ) , … , ( x n , y n y n ′ ) , … , ( x m , y m y m ′ )
值得注意的是,因为 deg h = deg f + deg g \deg h = \deg f + \deg g deg h = deg f + deg g n + m + 1 n + m + 1 n + m + 1 h ( x ) h(x) h ( x )
因此在点值表示法下,我们可以在线性的时间复杂度下完成加法和乘法运算。
复数与单位根
FFT 算法的最巧妙之一在于它很好的结合了复数的大量性质,本小节直接忽略复数的基础知识 。
复平面
任意一个复数 z ∈ Z , z = a + b i z \in \mathbb{Z}, z = a + bi z ∈ Z , z = a + bi z z z ( a , b ) (a, b) ( a , b )
定义复数 z z z ∣ z ∣ : = a 2 + b 2 |z| := \sqrt{a ^ 2 + b ^ 2} ∣ z ∣ := a 2 + b 2 r r r
定义复数 z z z arg z : = θ \arg z := \theta arg z := θ tan θ = b a \tan \theta = \frac{b}{a} tan θ = a b z z z x x x
根据高中所学,a = r cos θ , b = r sin θ a = r \cos \theta, b = r\sin \theta a = r cos θ , b = r sin θ 三角形式 :z = r ( cos θ + i sin θ ) z = r(\cos \theta + i \sin \theta) z = r ( cos θ + i sin θ )
直接引入棣莫弗定理 :复数相乘,模长相乘,幅角相加。
z 1 = r 1 ( cos θ 1 + i sin θ 1 ) , z 2 = r 2 ( cos θ 2 + i sin θ 2 ) z 1 × z 2 = r 1 × r 2 ( cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) ) z1 = r1(\cos \theta_1 + i \sin \theta_1), z2 = r2(\cos \theta_2 + i \sin \theta_2) \\
z1 \times z2 = r1 \times r2 \left ( \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2) \right )
z 1 = r 1 ( cos θ 1 + i sin θ 1 ) , z 2 = r 2 ( cos θ 2 + i sin θ 2 ) z 1 × z 2 = r 1 × r 2 ( cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) )
这个定理较为常见,但对于单位根的性质十分重要。
单位根
不妨钦定 ∣ z ∣ = 1 |z| = 1 ∣ z ∣ = 1 z z z z k = cos k θ + i sin k θ z ^ k = \cos ^ k \theta + i \sin ^ k \theta z k = cos k θ + i sin k θ z k z ^ k z k ( 1 , 0 ) (1, 0) ( 1 , 0 ) z z z θ \theta θ k k k
如果将这个单位圆 n n n n n n n n n ( 1 , 0 ) (1, 0) ( 1 , 0 ) n n n P 0 , P 1 , … , P n − 1 P_0, P_1, \dots,P_{n - 1} P 0 , P 1 , … , P n − 1 P 1 n P_1 ^ n P 1 n P i ( 1 < i < n ) P_i(1 \lt i \lt n) P i ( 1 < i < n )
写出它们的复平面坐标:P k = ( cos 2 k π n , i sin 2 k π n ) P_k = (\cos \frac{2k \pi}{n}, i \sin \frac{2k \pi}{n}) P k = ( cos n 2 kπ , i sin n 2 kπ ) ω n : = P 1 \omega_n := P_1 ω n := P 1 P k = ω n k = P 1 k P_k = \omega_n^k = P_1 ^ k P k = ω n k = P 1 k P k P_k P k 关于 n n n 。
这些点的性质如下:
存在循环,且循环周期为 n n n ω n k = ω n k t ( t > 0 ) \omega_n^k = \omega_n^{kt}(t \gt 0) ω n k = ω n k t ( t > 0 ) ω n k = ω n k + n t ( 0 ≤ k < n , t > 0 ) \omega_n^k = \omega_n^{k + nt}(0 \le k \lt n, t \gt 0) ω n k = ω n k + n t ( 0 ≤ k < n , t > 0 )
w n k = − w n k + n 2 ( 0 ≤ k < n 2 , n is even ) w_n^k = -w_n^{k + \frac{n}{2}}(0 \le k \lt \frac{n}{2}, n \text { is even}) w n k = − w n k + 2 n ( 0 ≤ k < 2 n , n is even ) ∀ w n k ( 0 ≤ k < n ) \forall w_n^k(0 \le k \lt n) ∀ w n k ( 0 ≤ k < n ) n n n n n n x n = 1 x^n = 1 x n = 1 n n n ( w n k ) n = 1 ( 0 ≤ k < n ) (w_n^k)^n = 1(0 \le k \lt n) ( w n k ) n = 1 ( 0 ≤ k < n )
着重注意第二、三性质,对于后续问题很重要。
本原单位根
本原单位根指的是集合 { ω n k ∣ 0 ≤ k < n , n ⊥ k } \{ \omega_n ^k \ | \ 0 \le k \lt n,n \perp k \ \} { ω n k ∣ 0 ≤ k < n , n ⊥ k } w n 1 w_n^1 w n 1
拉格朗日插值法
前面说到过,系数表示法和点值表示法可以进行转换,其中取值可以在 O ( deg f ) \mathcal{O}(\deg f) O ( deg f ) n n n O ( n 3 ) \mathcal{O}(n^3) O ( n 3 )
而拉格朗日插值法提供了一种特殊的方法,能让我们在 O ( n 2 ) \mathcal{O}(n ^ 2) O ( n 2 )
算法过程
由于点值表示法的点值可加性,我们可以把一个有 n + 1 n + 1 n + 1 f f f n + 1 n + 1 n + 1
f i ( x ) = { y i , if x = x i 0 , otherwise , 0 ≤ i ≤ n f_i(x) =
\begin{cases}
y_i, & \text{if } x = x_i \\
0, & \text{otherwise}
\end{cases}, \quad 0 \leq i \leq n
f i ( x ) = { y i , 0 , if x = x i otherwise , 0 ≤ i ≤ n
将这些多项式相加即为得到的原来多项式,容易证明这是对的,并且生成的多项式是唯一的。
那么如何构造出这些 f i ( x ) f_i(x) f i ( x ) ∏ j ≠ i x − x j \textstyle{\prod_{j \neq i} x - x_j} ∏ j = i x − x j x = x i x = x_i x = x i y i y_i y i ∏ j ≠ i 1 x i − x j \textstyle{\prod_{j \neq i} \frac{1}{x_i - x_j}} ∏ j = i x i − x j 1
f i ( x ) = y i ∏ j ≠ i x − x j x i − x j f_i(x) = y_i \prod_{j \neq i} \frac{x - x_j}{x_i - x_j}
f i ( x ) = y i j = i ∏ x i − x j x − x j
因此合成后可以得到目标函数:
f = ∑ i = 0 n f i = ∑ i = 0 n ( y i ∏ j ≠ i x − x j x i − x j ) f = \sum_{i = 0}^n f_i = \sum_{i = 0}^n \left ( y_i \prod_{j \neq i} \frac{x - x_j}{x_i - x_j} \right )
f = i = 0 ∑ n f i = i = 0 ∑ n y i j = i ∏ x i − x j x − x j
至于如何求出 f f f F ( x ) : = ∏ i = 0 n ( x − x i ) F(x) := \textstyle{\prod_{i = 0}^n (x - x_i)} F ( x ) := ∏ i = 0 n ( x − x i ) f i f_i f i O ( n ) \mathcal{O}(n) O ( n ) x − x i x - x_i x − x i f i f_i f i O ( n 2 ) \mathcal{O}(n ^ 2) O ( n 2 ) x x x
特殊情况
如果给出的点对是连续的,例如 ∀ i ( 0 ≤ i < n ) , x i = i \forall i(0 \le i \lt n), x_i = i ∀ i ( 0 ≤ i < n ) , x i = i O ( n ) \mathcal{O}(n) O ( n )
f = ∑ i = 0 n f i = ∑ i = 0 n y i ∏ j ≠ i x − j i − j f = \sum_{i = 0} ^ n f_i = \sum_{i = 0} ^ n y_i \prod_{j \neq i} \frac{x - j}{i - j}
f = i = 0 ∑ n f i = i = 0 ∑ n y i j = i ∏ i − j x − j
分子是经典的 ∏ j = 0 n x − j \textstyle{\prod_{j = 0}^n x - j} ∏ j = 0 n x − j x − i x - i x − i
分母因为连续同样可以预处理,分正负阶乘相乘即可,最终公式为:
f = ∑ i = 0 n f i = ∑ i = 0 n y i p r e i − 1 × s u f i + 1 ∏ j = 0 i − 1 ( i − j ) × ∏ j = i + 1 n ( i − j ) = ∑ i = 0 n p r e i − 1 × s u f i + 1 i ! × ( − 1 ) n − i + 1 × ( i − n + 1 ) ! \begin{aligned}
f = \sum_{i = 0} ^ n f_i &= \sum_{i = 0} ^ n y_i \frac{pre_{i - 1} \times suf_{i + 1}}{\prod_{j = 0} ^ {i - 1}(i - j) \times \prod_{j = i + 1} ^ {n} (i - j)} \\
&= \sum_{i = 0} ^ n \frac{pre_{i - 1} \times suf_{i + 1}}{i! \times (-1)^{n - i + 1} \times (i - n + 1)!}
\end{aligned}
f = i = 0 ∑ n f i = i = 0 ∑ n y i ∏ j = 0 i − 1 ( i − j ) × ∏ j = i + 1 n ( i − j ) p r e i − 1 × s u f i + 1 = i = 0 ∑ n i ! × ( − 1 ) n − i + 1 × ( i − n + 1 )! p r e i − 1 × s u f i + 1
由于 O ( 1 ) \mathcal{O}(1) O ( 1 ) f i f_i f i O ( n ) \mathcal{O}(n) O ( n )
代码
P4781 【模板】拉格朗日插值 - 洛谷
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 signed main () read (n, K); for (int i = 1 ; i <= n; i ++) read (x[i], y[i]); int ans = 0 ; for (int i = 1 ; i <= n; i ++) { int multi = 1 , div = 1 ; for (int j = 1 ; j <= n; j ++) { if (i == j) continue ; multi = multi * (K - x[j] + mod) % mod; div = div * (x[i] - x[j] + mod) % mod; } ans = (ans + multi * y[i] % mod * ksm (div, mod - 2 ) % mod) % mod; } cout << ans << '\n' ; return 0 ; }
快速傅里叶变换(FFT)
如果想从纯数学知识或者通信方面了解 FFT,请尝试先了解离散型傅里叶变换(DFT,Discrete Fourier Transform)的概念,FFT 是 DFT 的改进和转化(等我会了再说)。
而如果像我一样从计算机算法方面,只需要知道 FFT 可以用来优化多项式乘法就行了。
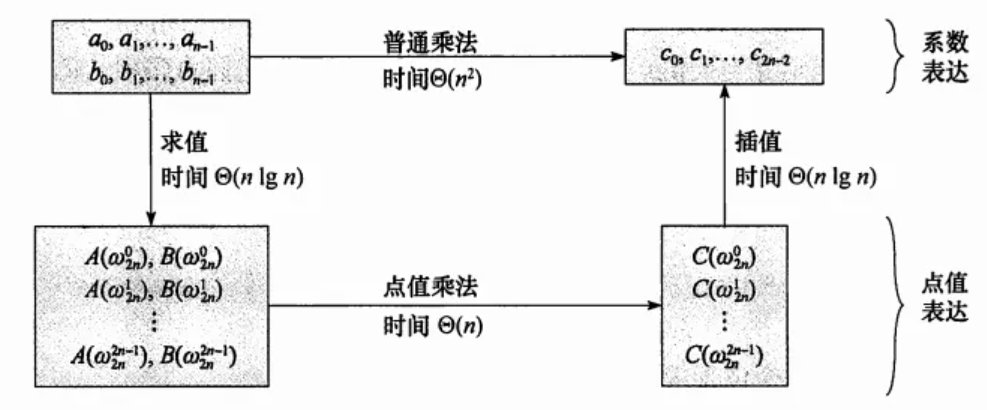
给定多项式 f f f g g g h = f × g h = f \times g h = f × g O ( n 2 ) \mathcal{O}(n ^ 2) O ( n 2 ) O ( n log n ) \mathcal{O}(n \log n) O ( n log n )
算法方向
前文提到过,系数表示法下的多项式乘法只能做到平方级别,然而点值表示法可以线性完成。这启发我们,如果我们对于多项式 f , g f,g f , g deg f + deg g \deg f + \deg g deg f + deg g deg f + deg g + 1 \deg f + \deg g + 1 deg f + deg g + 1 O ( n ) \mathcal{O}(n) O ( n ) O ( n 2 ) \mathcal{O}(n ^ 2) O ( n 2 )
不过很有启发性,我们能否找到一种方法,使得预先的求值可以做到 O ( n polylog ( n ) ) \mathcal{O}(n\operatorname{polylog}(n)) O ( n polylog ( n ))
第一次折半
有的。
考虑一个极其普通的二次多项式 f ( x ) = x 2 f(x) = x ^ 2 f ( x ) = x 2 x = { 0 , 1 , 2 } , f ( x ) = { 0 , 2 , 4 } x = \{ 0, 1, 2\}, f(x) = \{ 0, 2, 4\} x = { 0 , 1 , 2 } , f ( x ) = { 0 , 2 , 4 } O ( n 2 ) O(n ^ 2) O ( n 2 ) x = { − 1 , 0 , 1 } x = \{-1, 0, 1\} x = { − 1 , 0 , 1 } f ( − 1 ) = f ( − ( 1 ) ) = f ( 1 ) = 1 f(-1) = f(-(1)) = f(1) = 1 f ( − 1 ) = f ( − ( 1 )) = f ( 1 ) = 1 − 1 , 1 -1,1 − 1 , 1 x x x
不仅是偶函数,奇函数也如此,例如 f ( x ) = x 3 + x f(x) = x ^ 3 + x f ( x ) = x 3 + x f ( − 1 ) = f ( − ( 1 ) ) = − f ( 1 ) f(-1) = f(-(1)) = -f(1) f ( − 1 ) = f ( − ( 1 )) = − f ( 1 )
既然发现了这个性质,我们推广到普遍的多项式 f ( x ) = ∑ i = 0 n a i x i f(x) = \textstyle{\sum_{i = 0}^n a_ix^i} f ( x ) = ∑ i = 0 n a i x i
f ( x ) = ∑ i = 0 n a i x i f e ( x ) : = a 0 x 0 + a 2 x 2 + a 4 x 4 + … , f o ( x ) : = a 1 x 1 + a 3 x 3 + a 5 x 5 + … ∴ f ( x ) = f e ( x ) + f o ( x ) f(x) = \sum_{i = 0}^n a_ix^i \\
f_e(x) := a_0x^0 + a_2x^2 + a_4x^4 + \dots,f_o(x) := a_1x^1 + a_3x^3 + a_5x^5 + \dots \\
\therefore f(x) = f_e(x) + f_o(x)
f ( x ) = i = 0 ∑ n a i x i f e ( x ) := a 0 x 0 + a 2 x 2 + a 4 x 4 + … , f o ( x ) := a 1 x 1 + a 3 x 3 + a 5 x 5 + … ∴ f ( x ) = f e ( x ) + f o ( x )
根据高中所学,显然 f e ( x ) f_e(x) f e ( x ) f o ( x ) f_o(x) f o ( x ) ⌈ n 2 ⌉ \lceil \frac{n}{2}\rceil ⌈ 2 n ⌉ x x x f e f_e f e f o f_o f o
{ f ( x ) = f e ( x ) + f o ( x ) f ( − x ) = f e ( x ) − f o ( x ) \begin{cases}
f(x) = f_e(x) + f_o(x) \\
f(-x) = f_e(x) - f_o(x)
\end{cases}
{ f ( x ) = f e ( x ) + f o ( x ) f ( − x ) = f e ( x ) − f o ( x )
讨论此时的时间复杂度,f e f_e f e f o f_o f o O ( 2 × ⌈ n 2 ⌉ ⌈ n 2 ⌉ ) = O ( n 2 2 ) = O ( n 2 ) \mathcal{O}(2 \times \lceil \frac{n}{2}\rceil \lceil \frac{n}{2}\rceil) = \mathcal{O}(\frac{n ^ 2}{2}) = \mathcal{O}(n ^ 2) O ( 2 × ⌈ 2 n ⌉ ⌈ 2 n ⌉) = O ( 2 n 2 ) = O ( n 2 ) log n \log n log n T ( n ) = 2 × T ( n 2 ) + O ( n ) = O ( n log n ) T(n) = 2 \times T(\frac{n}{2}) + \mathcal{O}(n) = \mathcal{O}(n \log n) T ( n ) = 2 × T ( 2 n ) + O ( n ) = O ( n log n )
继续递归
在第一层递归时,我们选取了互为相反数作为点值,从而将求解多项式 f ( x ) f(x) f ( x ) f e ( x ) f_e(x) f e ( x ) f o ( x ) f_o(x) f o ( x )
对于偶函数 f e ( x ) = a 0 + a 2 x 2 + a 4 x 4 + … f_e(x) = a_0 + a_2x^2 + a_4x^4 + \dots f e ( x ) = a 0 + a 2 x 2 + a 4 x 4 + … f e ′ ( x ) : = f e ( x 2 ) = a 0 + a 2 x + a 4 x 2 + … f_e'(x) := f_e(x ^ 2) = a_0 + a_2x + a_4x^2 + \dots f e ′ ( x ) := f e ( x 2 ) = a 0 + a 2 x + a 4 x 2 + … f ( x ) f(x) f ( x ) ( p , − q ) (p, -q) ( p , − q ) f e ′ ( x ) = f e ( x 2 ) f_e'(x) = f_e(x ^ 2) f e ′ ( x ) = f e ( x 2 ) p 2 = q 2 p ^ 2 = q ^ 2 p 2 = q 2
换句话说,目前我们要找到一对不同数 ( p , − p ) (p, -p) ( p , − p ) p 2 = − ( − p ) 2 p ^ 2 = -(-p) ^ 2 p 2 = − ( − p ) 2 i i i i 2 = − ( − i ) 2 i^2 = - (-i)^2 i 2 = − ( − i ) 2 f ( x ) = x 3 + x 2 − x − 1 f(x) = x ^ 3 + x ^ 2 - x - 1 f ( x ) = x 3 + x 2 − x − 1 ( x 1 , − x 1 ) , ( x 2 , − x 2 ) (x1, -x1), (x2, -x2) ( x 1 , − x 1 ) , ( x 2 , − x 2 ) ( x 1 2 , x 2 2 ) (x_1^2, x_2^2) ( x 1 2 , x 2 2 ) ( 1 , i , − 1 , − i ) (1, i, -1, -i) ( 1 , i , − 1 , − i ) ( 1 , i , − 1 , − i ) (1, i, -1, -i) ( 1 , i , − 1 , − i ) f e , f o f_e, f_o f e , f o ( 1 2 , i 2 ) (1^2, i^2) ( 1 2 , i 2 ) x = 1 4 = i 4 x = 1 ^ 4 = i ^ 4 x = 1 4 = i 4
继续拓展至 n n n n ← 2 ⌈ log n ⌉ n \gets 2 ^ {\lceil \log n \rceil} n ← 2 ⌈ l o g n ⌉
如何选择 ( x 1 , − x 1 , x 2 , − x 2 , x 3 , − x 3 , x 4 , − x 4 ) (x_1, -x_1, x_2, -x_2, x_3, -x_3, x_4, -x_4) ( x 1 , − x 1 , x 2 , − x 2 , x 3 , − x 3 , x 4 , − x 4 ) x k n = 1 x_k^n = 1 x k n = 1
不仅如此,w n k = − w n k + n 2 ( 0 ≤ k < n 2 , n is even ) w_n^k = -w_n^{k + \frac{n}{2}}(0 \le k \lt \frac{n}{2}, n \text { is even}) w n k = − w n k + 2 n ( 0 ≤ k < 2 n , n is even ) ( x 1 , x 2 , x 3 , x 4 ) (x1, x2, x3, x4) ( x 1 , x 2 , x 3 , x 4 )
当 w n k w_n^k w n k w n k → w n k 2 = ( w n k ) 2 w_n^k \to w_n^{k^2} = (w_n^k)^2 w n k → w n k 2 = ( w n k ) 2 ( w n k ) 2 = w n 2 k (w_n^k) ^ 2 = w_{\frac{n}{2}}^k ( w n k ) 2 = w 2 n k
像这样,最开始我们给多项式设定的 n n n n n n n n n ω 0 , ω 1 , … , ω n − 1 \omega_0, \omega_1, \dots, \omega_{n - 1} ω 0 , ω 1 , … , ω n − 1 1 1 1 O ( n ) \mathcal{O}(n) O ( n ) log n \log n log n O ( n ) \mathcal{O}(n) O ( n )
大致流程
根据单位根的特殊性质证明了可行性,我们再梳理一遍 FFT 的大致流程。
为方便递归,同时保持对称性质,令 L ← 2 ⌈ log n + m + 1 ⌉ L \gets 2 ^ {\lceil \log n + m + 1 \rceil} L ← 2 ⌈ l o g n + m + 1 ⌉ 0 0 0
设当前递归的多项式为 b o r d e r border b or d er b o r d e r = 1 border = 1 b or d er = 1 a 0 a_0 a 0
否则处理出所有的单位根 w b o r d e r k ( 0 ≤ k < b o r d e r 2 ) w_{border}^k (0 \le k \lt \frac{border}{2}) w b or d er k ( 0 ≤ k < 2 b or d er ) f ‘ ( x ) = f e ′ ( x ) + f o ′ ( x ) f‘(x) = f_e'(x) + f_o'(x) f ‘ ( x ) = f e ′ ( x ) + f o ′ ( x )
f ’ ( w b o r d e r k ) = f e ′ ( w b o r d e r 2 k ) + w b o r d e r k × f o ′ ( w b o r d e r 2 k ) f’(w_{border}^k) = f_e'(w_{border}^{2k}) + w_{border}^k \times f_o'(w_{border}^{2k})
f ’ ( w b or d er k ) = f e ′ ( w b or d er 2 k ) + w b or d er k × f o ′ ( w b or d er 2 k )
计算出所有 0 < k < b o r d e r 2 0 \lt k \lt \frac{border}{2} 0 < k < 2 b or d er f ′ ( ω b o r d e r k ) f'(\omega_{border}^{k}) f ′ ( ω b or d er k ) w n k = − w n k + n 2 w_n^k = -w_n^{k + \frac{n}{2}} w n k = − w n k + 2 n f ′ ( ω b o r d e r k + b o r d e r 2 ) f'(\omega_{border}^{k + \frac{border}{2}}) f ′ ( ω b or d er k + 2 b or d er )
f ′ ( w b o r d e r k + b o r d e r 2 ) = f e ′ ( w b o r d e r 2 k + b o r d e r ) + w b o r d e r k + b o r d e r 2 × f o ′ ( w b o r d e r 2 k + b o r d e r ) = f e ′ ( w b o r d e r 2 k × w b o r d e r b o r d e r ) − w b o r d e r k × f o ′ ( w b o r d e r 2 k × w b o r d e r b o r d e r ) = f e ′ ( w b o r d e r 2 k ) − w b o r d e r k × f o ′ ( w b o r d e r 2 k ) \begin{aligned}
f'(w_{border}^{k + \frac{border}{2}}) &= f'_e(w_{border}^{2k + border}) + w_{border}^{k + \frac{border}{2}} \times f'_o(w_{border}^{2k + border}) \\
&= f_e'(w_{border}^{2k} \times w_{border}^{border}) - w_{border}^k \times f_o'(w_{border}^{2k} \times w_{border}^{border}) \\
&= f_e'(w_{border}^{2k}) - w_{border}^k \times f_o'(w_{border}^{2k})
\end{aligned}
f ′ ( w b or d er k + 2 b or d er ) = f e ′ ( w b or d er 2 k + b or d er ) + w b or d er k + 2 b or d er × f o ′ ( w b or d er 2 k + b or d er ) = f e ′ ( w b or d er 2 k × w b or d er b or d er ) − w b or d er k × f o ′ ( w b or d er 2 k × w b or d er b or d er ) = f e ′ ( w b or d er 2 k ) − w b or d er k × f o ′ ( w b or d er 2 k )
通过这两个等式:
{ f ′ ( w b o r d e r k ) = f e ′ ( w b o r d e r 2 k ) + w b o r d e r k × f o ′ ( w b o r d e r 2 k ) f ′ ( w b o r d e r k + b o r d e r 2 ) = f e ′ ( w b o r d e r 2 k ) − w b o r d e r k × f o ′ ( w b o r d e r 2 k ) ( 0 ≤ k < b o r d e r 2 ) \begin{cases}
f'(w_{border}^k) = f_e'(w_{border}^{2k}) + w_{border}^k \times f_o'(w_{border}^{2k}) \\
f'(w_{border}^{k + \frac{border}{2}}) = f_e'(w_{border}^{2k}) - w_{border}^k \times f_o'(w_{border}^{2k})
\end{cases} (0 \le k \lt \frac{border}{2})
{ f ′ ( w b or d er k ) = f e ′ ( w b or d er 2 k ) + w b or d er k × f o ′ ( w b or d er 2 k ) f ′ ( w b or d er k + 2 b or d er ) = f e ′ ( w b or d er 2 k ) − w b or d er k × f o ′ ( w b or d er 2 k ) ( 0 ≤ k < 2 b or d er )
因此猜想成立,时间复杂度:T ( n ) = 2 × T ( n 2 ) + O ( n ) = O ( n log n ) T(n) = 2 \times T(\frac{n}{2}) + \mathcal{O}(n) = \mathcal{O}(n \log n) T ( n ) = 2 × T ( 2 n ) + O ( n ) = O ( n log n )
1 2 3 4 5 6 7 8 9 10 11 12 13 void FFT (int border, vector<Complex> &A, int type) if (border == 1 ) return ; vector<Complex> F (border / 2 ) , G (border / 2 ) ; for (int i = 0 ; i < border; i += 2 ) F[i >> 1 ] = A[i], G[i >> 1 ] = A[i + 1 ]; FFT (border / 2 , F, type), FFT (border / 2 , G, type); Complex base = Complex (cos (2.0 * PI / border), sin (2.0 * PI / border) * type), cur = Complex (1 , 0 ); for (int i = 0 ; i < border / 2 ; i ++, cur = cur * base) A[i] = F[i] + G[i] * cur, A[i + (border / 2 )] = F[i] - G[i] * cur; }
迭代优化
虽然我们的递归算法很好地实现了 FFT,将时间复杂度控制在了 O ( n log n ) \mathcal{O}(n \log n) O ( n log n )
有的,我们称之为蝴蝶变换。
由于从下往上递归,原先的递归版本中递归前的这么一句话:
1 for (int i = 0 ; i < border; i += 2 ) F[i >> 1 ] = A[i], G[i >> 1 ] = A[i + 1 ];
要求我们在迭代前预处理出来,换句话说,对于原多项式系数序列(这里钦定 n = 16 n = 16 n = 16
( a 0 , a 1 , a 2 , a 3 , a 4 , a 5 , a 6 , a 7 , a 8 , a 9 , a 10 , a 11 , a 12 , a 13 , a 14 , a 15 ) ⇒ ( a 0 , a 2 , a 4 , a 6 , a 8 , a 10 , a 12 , a 14 ) , ( a 1 , a 3 , a 5 , a 7 , a 9 , a 11 , a 13 , a 15 ) ⇒ ⋯ ⇒ ( a 0 , a 8 ) , ( a 2 , a 10 ) , ( a 4 , a 12 ) , ( a 6 , a 14 ) , ( a 1 , a 9 ) , ( a 3 , a 11 ) , ( a 5 , a 13 ) , ( a 7 , a 15 ) (a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7, a_8, a_9, a_{10}, a_{11}, a_{12}, a_{13}, a_{14}, a_{15}) \Rightarrow \\
(a_0, a_2, a_4, a_6, a_8, a_{10}, a_{12}, a_{14}), (a_1, a_3, a_5, a_7, a_9, a_{11}, a_{13}, a_{15}) \Rightarrow \\
\dots \Rightarrow \\
(a_0, a_8), (a_2, a_{10}), (a_4, a_{12}), (a_6, a_{14}), (a_1, a_9), (a_3, a_{11}), (a_5, a_{13}), (a_7, a_{15})
( a 0 , a 1 , a 2 , a 3 , a 4 , a 5 , a 6 , a 7 , a 8 , a 9 , a 10 , a 11 , a 12 , a 13 , a 14 , a 15 ) ⇒ ( a 0 , a 2 , a 4 , a 6 , a 8 , a 10 , a 12 , a 14 ) , ( a 1 , a 3 , a 5 , a 7 , a 9 , a 11 , a 13 , a 15 ) ⇒ ⋯ ⇒ ( a 0 , a 8 ) , ( a 2 , a 10 ) , ( a 4 , a 12 ) , ( a 6 , a 14 ) , ( a 1 , a 9 ) , ( a 3 , a 11 ) , ( a 5 , a 13 ) , ( a 7 , a 15 )
重排成以上序列。
i (十进制) i (二进制) r [ i ] (十进制) r [ i ] (二进制) 1 0001 8 1000 2 0010 4 0100 3 0011 12 1100 4 0100 2 0010 5 0101 10 1010 6 0110 6 0110 7 0111 14 1110 8 1000 1 0001 9 1001 9 1001 10 1010 5 0101 11 1011 13 1101 12 1100 3 0011 13 1101 11 1011 14 1110 7 0111 15 1111 15 1111 \begin{array}{|c|c|c|c|}
\hline
i \text{ (十进制)} & i \text{ (二进制)} & r[i] \text{ (十进制)} & r[i] \text{ (二进制)} \\
\hline
1 & 0001 & 8 & 1000 \\
2 & 0010 & 4 & 0100 \\
3 & 0011 & 12 & 1100 \\
4 & 0100 & 2 & 0010 \\
5 & 0101 & 10 & 1010 \\
6 & 0110 & 6 & 0110 \\
7 & 0111 & 14 & 1110 \\
8 & 1000 & 1 & 0001 \\
9 & 1001 & 9 & 1001 \\
10 & 1010 & 5 & 0101 \\
11 & 1011 & 13 & 1101 \\
12 & 1100 & 3 & 0011 \\
13 & 1101 & 11 & 1011 \\
14 & 1110 & 7 & 0111 \\
15 & 1111 & 15 & 1111 \\
\hline
\end{array}
i ( 十进制 ) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 i ( 二进制 ) 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 r [ i ] ( 十进制 ) 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15 r [ i ] ( 二进制 ) 1000 0100 1100 0010 1010 0110 1110 0001 1001 0101 1101 0011 1011 0111 1111
列出表格后凭借惊人的注意力发现 i i i r i r_i r i O ( n ) \mathcal{O}(n) O ( n ) r i r_i r i
1 2 for (int i = 0 ; i < T; i ++) R[i] = (R[i >> 1 ] >> 1 ) | (i & 1 ? T >> 1 : 0 );for (int i = 0 ; i < T; i ++) if (i < R[i]) swap (A[i], A[R[i]]);
这就是蝴蝶变换,同样迭代实现的 FFT 算法也可以完成了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void FFT (vector<Complex> &A, int type) vector<int > R (T) ; for (int i = 0 ; i < T; i ++) R[i] = (R[i >> 1 ] >> 1 ) | (i & 1 ? T >> 1 : 0 ); for (int i = 0 ; i < T; i ++) if (i < R[i]) swap (A[i], A[R[i]]); for (int cur = 1 ; cur < T; cur <<= 1 ) { Complex base (cos(PI / cur), sin(PI / cur) * type) ; static vector<Complex> comp (T + 1 ) comp[0 ] = Complex (1 , 0 ); for (int i = 1 ; i < cur; i ++) comp[i] = comp[i - 1 ] * base; for (int i = 0 ; i < T; i += cur << 1 ) for (int j = 0 ; j < cur; j ++) { Complex tempx = A[i | j], tempy = A[i | j | cur] * comp[j]; A[i | j] = tempx + tempy, A[i | j | cur] = tempx - tempy; } } }
以上过程就称为 对长度为 n n n f f f 。
快速傅里叶逆变换(IFFT)
结束了么,并没有。我们在 O ( n log n ) \mathcal{O}(n \log n) O ( n log n ) O ( n ) \mathcal{O}(n) O ( n ) O ( n ) \mathcal{O}(n) O ( n ) 快速傅里叶逆变换 (Inverse Fast Fourier Transform ),也就是 FFT 的逆操作。
讲到 IFFT 了就不得不引入范德蒙德矩阵了,作为和多项式紧密联系的矩阵,我们通过矩阵乘法可以求出多项式的点值:
P ( x ) = p 0 + p 1 x 1 + p 2 x 2 + ⋯ + p n − 1 x n − 1 [ P ( x 0 ) P ( x 1 ) P ( x 2 ) ⋮ P ( x n − 1 ) ] = [ 1 x 0 x 0 2 ⋯ x 0 n − 1 1 x 1 x 1 2 ⋯ x 1 n − 1 1 x 2 x 2 2 ⋯ x 2 n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n − 1 x n − 1 2 ⋯ x n − 1 n − 1 ] [ p 0 p 1 p 2 ⋮ p n − 1 ] P(x) = p_0 + p_1x^1 +p_2x^2+ \dots + p_{n - 1}x^{n - 1}\\
\begin{bmatrix}
P(x_0) \\
P(x_1) \\
P(x_2) \\
\vdots \\
P(x_{n-1})
\end{bmatrix}
=
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\
1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\
1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1}
\end{bmatrix}
\begin{bmatrix}
p_0 \\
p_1 \\
p_2 \\
\vdots \\
p_{n-1}
\end{bmatrix}
P ( x ) = p 0 + p 1 x 1 + p 2 x 2 + ⋯ + p n − 1 x n − 1 P ( x 0 ) P ( x 1 ) P ( x 2 ) ⋮ P ( x n − 1 ) = 1 1 1 ⋮ 1 x 0 x 1 x 2 ⋮ x n − 1 x 0 2 x 1 2 x 2 2 ⋮ x n − 1 2 ⋯ ⋯ ⋯ ⋱ ⋯ x 0 n − 1 x 1 n − 1 x 2 n − 1 ⋮ x n − 1 n − 1 p 0 p 1 p 2 ⋮ p n − 1
下面令:
F = [ 1 x 0 x 0 2 ⋯ x 0 n − 1 1 x 1 x 1 2 ⋯ x 1 n − 1 1 x 2 x 2 2 ⋯ x 2 n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n − 1 x n − 1 2 ⋯ x n − 1 n − 1 ] \mathcal{F} =
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\
1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\
1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1}
\end{bmatrix}
F = 1 1 1 ⋮ 1 x 0 x 1 x 2 ⋮ x n − 1 x 0 2 x 1 2 x 2 2 ⋮ x n − 1 2 ⋯ ⋯ ⋯ ⋱ ⋯ x 0 n − 1 x 1 n − 1 x 2 n − 1 ⋮ x n − 1 n − 1
既然范德蒙德矩阵可以用来求多项式点值,那么它的逆 F − 1 \mathcal{F}^{-1} F − 1
考虑求出 F − 1 \mathcal{F}^{-1} F − 1
f = ∑ i = 0 n f i = ∑ i = 0 n ( y i ∏ j ≠ i x − x j x i − x j ) L i : = ∏ j ≠ i x − x j x i − x j f = \sum_{i = 0}^n f_i = \sum_{i = 0}^n \left ( y_i \prod_{j \neq i} \frac{x - x_j}{x_i - x_j} \right ) \\
L_i := \prod_{j \neq i} \frac{x - x_j}{x_i - x_j}
f = i = 0 ∑ n f i = i = 0 ∑ n y i j = i ∏ x i − x j x − x j L i := j = i ∏ x i − x j x − x j
其中 L i L_i L i
L i ( x ) = { 1 if x = x j 0 otherwise L_i(x) =
\begin{cases}
1 & \text{if } x = x_j \\
0 & \text{otherwise}
\end{cases}
L i ( x ) = { 1 0 if x = x j otherwise
不难发现,这 n n n I \mathcal{I} I
F × F − 1 = I \mathcal{F} \times \mathcal{F}^{-1} = \mathcal{I}
F × F − 1 = I
解出来得到:
( F − 1 ) i j = c j ( x i − x j ) c i for i ≠ j , ( F − 1 ) i i = 1 c i c i = ∏ 0 ≤ k ≤ n − 1 k ≠ i ( x i − x k ) = ( x i − x 0 ) ( x i − x 1 ) ⋯ ( x i − x i − 1 ) ( x i − x i + 1 ) ⋯ ( x i − x n − 1 ) (\mathcal{F}^{-1})_{ij} = \frac{ c_j }{ (x_i - x_j)c_i } \quad \text{for } i \neq j, \quad (\mathcal{F}^{-1})_{ii} = \frac{1}{c_i} \\
c_i = \prod_{\substack{0 \leq k \leq n-1 \\ k \neq i}} (x_i - x_k) = (x_i - x_0)(x_i - x_1) \cdots (x_i - x_{i-1})(x_i - x_{i+1}) \cdots (x_i - x_{n-1})
( F − 1 ) ij = ( x i − x j ) c i c j for i = j , ( F − 1 ) ii = c i 1 c i = 0 ≤ k ≤ n − 1 k = i ∏ ( x i − x k ) = ( x i − x 0 ) ( x i − x 1 ) ⋯ ( x i − x i − 1 ) ( x i − x i + 1 ) ⋯ ( x i − x n − 1 )
c i c_i c i L i ( x ) L_i(x) L i ( x )
看似没有什么特性,但是我们把单位根代入进去,这就是 FFT 的矩阵:
ω : = ω N , N : = b o r d e r F = [ 1 1 1 ⋯ 1 1 ω ω 2 ⋯ ω N − 1 1 ω 2 ω 4 ⋯ ω 2 ( N − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ω N − 1 ω 2 ( N − 1 ) ⋯ ω ( N − 1 ) ( N − 1 ) ] \omega := \omega_{N}, N := border\\
\mathcal{F} =
\begin{bmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & \omega & \omega^2 & \cdots & \omega^{N-1} \\
1 & \omega^2 & \omega^4 & \cdots & \omega^{2(N-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \omega^{N-1} & \omega^{2(N-1)} & \cdots & \omega^{(N-1)(N-1)}
\end{bmatrix}
ω := ω N , N := b or d er F = 1 1 1 ⋮ 1 1 ω ω 2 ⋮ ω N − 1 1 ω 2 ω 4 ⋮ ω 2 ( N − 1 ) ⋯ ⋯ ⋯ ⋱ ⋯ 1 ω N − 1 ω 2 ( N − 1 ) ⋮ ω ( N − 1 ) ( N − 1 )
算出它的逆 F − 1 \mathcal{F}^{-1} F − 1
F − 1 = 1 N [ 1 1 1 ⋯ 1 1 ω − 1 ω − 2 ⋯ ω − ( N − 1 ) 1 ω − 2 ω − 4 ⋯ ω − 2 ( N − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ω − ( N − 1 ) ω − 2 ( N − 1 ) ⋯ ω − ( N − 1 ) ( N − 1 ) ] \mathcal{F}^{-1} = \frac{1}{N} \begin{bmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & \omega^{-1} & \omega^{-2} & \cdots & \omega^{-(N-1)} \\
1 & \omega^{-2} & \omega^{-4} & \cdots & \omega^{-2(N-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \omega^{-(N-1)} & \omega^{-2(N-1)} & \cdots & \omega^{-(N-1)(N-1)}
\end{bmatrix}
F − 1 = N 1 1 1 1 ⋮ 1 1 ω − 1 ω − 2 ⋮ ω − ( N − 1 ) 1 ω − 2 ω − 4 ⋮ ω − 2 ( N − 1 ) ⋯ ⋯ ⋯ ⋱ ⋯ 1 ω − ( N − 1 ) ω − 2 ( N − 1 ) ⋮ ω − ( N − 1 ) ( N − 1 )
也就是说,我们把 FFT 算法中的所有 ω \omega ω ω − 1 \omega^{-1} ω − 1 1 1 1 ω − 1 = ω ˉ \omega^{-1} = \bar{\omega} ω − 1 = ω ˉ 1 N \frac{1}{N} N 1
如果你看不懂上述矩阵,我们可以逆推出来:
对于多项式 f ( x ) = ∑ i = 0 n − 1 a i x i f(x) = \textstyle{\sum_{i = 0}^{n - 1}} a_ix^i f ( x ) = ∑ i = 0 n − 1 a i x i g ( x ) = ∑ i = 0 n − 1 b i x i g(x) = \textstyle{\sum_{i = 0}^{n - 1} b_ix^i} g ( x ) = ∑ i = 0 n − 1 b i x i b i = ∑ k = 0 n − 1 a k ( ω n k ) i b_i = \textstyle{\sum_{k = 0}^{n - 1}a_k (\omega_n^{k})^i} b i = ∑ k = 0 n − 1 a k ( ω n k ) i ω \omega ω ω − 1 \omega^{-1} ω − 1 g g g h ( x ) h(x) h ( x )
h ( x ) = ∑ i = 0 n − 1 c i x i c i = ∑ k = 0 n − 1 b k ( ω n − k ) i = ∑ k = 0 n − 1 ( ∑ j = 0 n − 1 a j ( ω n j ) k ) ( ω n − k ) i = ∑ j = 0 n − 1 ( a j ∑ k = 0 n − 1 ( ω n j − i ) k ) h(x) = \sum_{i = 0}^{n - 1} c_ix^i \\
\begin{aligned}
c_i &= \sum_{k = 0}^{n - 1} b_k (\omega_n^{-k})^i \\
&= \sum_{k = 0}^{n - 1} \left ( \sum_{j = 0}^{n - 1} a_j(\omega_n^j)^k \right )(\omega_n^{-k})^i \\
&= \sum_{j = 0}^{n - 1} \left ( a_j \sum_{k = 0}^{n - 1} (\omega_{n}^{j - i})^k \right )
\end{aligned}
h ( x ) = i = 0 ∑ n − 1 c i x i c i = k = 0 ∑ n − 1 b k ( ω n − k ) i = k = 0 ∑ n − 1 ( j = 0 ∑ n − 1 a j ( ω n j ) k ) ( ω n − k ) i = j = 0 ∑ n − 1 ( a j k = 0 ∑ n − 1 ( ω n j − i ) k )
同理求出可以,通过拉格朗日插值法的基函数也可以证明:当 i = j i = j i = j c i c_i c i
c i = n a i ⇒ a i = c i n c_i = n a_i \Rightarrow a_i = \frac{c_i}{n}
c i = n a i ⇒ a i = n c i
我们在求完之后对整个 FFT 得到的序列除以 n n n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void FFT (vector<Complex> &A, int type) vector<int > R (T) ; for (int i = 0 ; i < T; i ++) R[i] = (R[i >> 1 ] >> 1 ) | (i & 1 ? T >> 1 : 0 ); for (int i = 0 ; i < T; i ++) if (i < R[i]) swap (A[i], A[R[i]]); for (int cur = 1 ; cur < T; cur <<= 1 ) { Complex base (cos(PI / cur), sin(PI / cur) * type) ; static vector<Complex> comp (T + 1 ) comp[0 ] = Complex (1 , 0 ); for (int i = 1 ; i < cur; i ++) comp[i] = comp[i - 1 ] * base; for (int i = 0 ; i < T; i += cur << 1 ) for (int j = 0 ; j < cur; j ++) { Complex tempx = A[i | j], tempy = A[i | j | cur] * comp[j]; A[i | j] = tempx + tempy, A[i | j | cur] = tempx - tempy; } } }
快速多项式乘法
这自然是 FFT 和 IFFT 在信息竞赛最常见的应用,大致流程和代码已经给出。
P3803 【模板】多项式乘法(FFT) - 洛谷 代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 int T = 1 , n, m;void FFT (vector<Complex> &A, int type) vector<int > R (T) ; for (int i = 0 ; i < T; i ++) R[i] = (R[i >> 1 ] >> 1 ) | (i & 1 ? T >> 1 : 0 ); for (int i = 0 ; i < T; i ++) if (i < R[i]) swap (A[i], A[R[i]]); for (int cur = 1 ; cur < T; cur <<= 1 ) { Complex base (cos(PI / cur), sin(PI / cur) * type) ; static vector<Complex> comp (T + 1 ) comp[0 ] = Complex (1 , 0 ); for (int i = 1 ; i < cur; i ++) comp[i] = comp[i - 1 ] * base; for (int i = 0 ; i < T; i += cur << 1 ) for (int j = 0 ; j < cur; j ++) { Complex tempx = A[i | j], tempy = A[i | j | cur] * comp[j]; A[i | j] = tempx + tempy, A[i | j | cur] = tempx - tempy; } } } signed main () read (n, m); while (T <= n + m) T <<= 1 ; vector<Complex> F (T) , G (T) ; for (int i = 0 , x; i <= n; i ++) read (x), F[i].a = x; for (int i = 0 , x; i <= m; i ++) read (x), G[i].a = x; FFT (F, 1 ), FFT (G, 1 ); vector<Complex> H (T) ; for (int i = 0 ; i < T; i++) H[i] = F[i] * G[i]; FFT (H, -1 ); for (int i = 0 ; i <= n + m; i++) write ((int )round (H[i].a / T), ' ' ); return 0 ; }
快速数论变换(FNTT)
阅读前请自行了解 【笔记】阶和原根 | Thy’s Blog 。
FNTT 的优势
在了解了 FFT 之后,不难发现虽然算法的时间复杂度达到了 O ( n log n ) \mathcal{O}(n \log n) O ( n log n ) double 类型。这显然是非常不好的,在 n n n
那么有什么其它的东西可以代替复数和单位根,精度高,运算快,满足竞赛需求,并且允许我们像类似复数运算那样完成 FFT 算法呢?
有的,兄弟有的,它叫做原根,被广泛用于快速数论变换 (Fast Number Theoretic Transform )。
原根
这里再提一下原根是什么:在模数域 Z m \mathbb{Z}_m Z m g ∈ Z m g \in \mathbb{Z}_m g ∈ Z m g ⊥ m g \perp m g ⊥ m δ m ( g ) = φ ( m ) \delta_m(g) = \varphi(m) δ m ( g ) = φ ( m ) g g g m m m
我们定义 ω n : = g φ ( m ) / n \omega_n := g^{\varphi(m) / n} ω n := g φ ( m ) / n
那原根为什么可以用来替代复数域中的单位根呢,它有如下几个性质:
ω n \omega_n ω n n n n n n n
ω n \omega_n ω n ω n ⊥ m \omega_n \perp m ω n ⊥ m ω n k \omega_n^k ω n k ω n − k \omega_n^{-k} ω n − k
ω n \omega_n ω n ω n k = ω n k + n \omega_n^k = \omega_n^{k + n} ω n k = ω n k + n ω n − k = ω n n − k \omega_n^{-k} = \omega_n^{n - k} ω n − k = ω n n − k
具有迭代传递性质,即 ω n k = ω 2 n 2 k \omega_n^k = \omega_{2n}^{2k} ω n k = ω 2 n 2 k
中心对称性质:
ω n n ≡ ω n n / 2 ω n n / 2 ≡ 1 ( m o d m ) ⇒ ω n n / 2 ≡ − 1 ( m o d m ) ⇒ ω n k + n / 2 ≡ − ω n k ( m o d m ) ⇒ ω n k = − ω n k + n / 2 \omega_n^n \equiv \omega_n^{n / 2}\omega_n^{n / 2} \equiv 1 \pmod m \Rightarrow \omega_n^{n / 2} \equiv -1 \pmod m \Rightarrow \omega_n^{k + n / 2} \equiv -\omega_n^k \pmod m \Rightarrow \omega_n^k = -\omega_n^{k + n / 2}
ω n n ≡ ω n n /2 ω n n /2 ≡ 1 ( mod m ) ⇒ ω n n /2 ≡ − 1 ( mod m ) ⇒ ω n k + n /2 ≡ − ω n k ( mod m ) ⇒ ω n k = − ω n k + n /2
因为存在逆元,因此 IFNTT 也可以使用。
因此原根完美代替了复数单位根的存在,那么这个模数取多少呢?
关于 998244353
NTT 最常用的模数为 998244353 998244353 998244353 469762049 , 1004535809 , 2013265921 469762049,1004535809,2013265921 469762049 , 1004535809 , 2013265921 998244353 998244353 998244353
998244353 < 1 0 9 , 2 × 998244353 < INT_MAX , 99824435 3 2 < LONG_LONG_MAX 998244353 \lt 10^9,2 \times 998244353 \lt \text{INT\_MAX},998244353^2 \lt \text{LONG\_LONG\_MAX} 998244353 < 1 0 9 , 2 × 998244353 < INT_MAX , 99824435 3 2 < LONG_LONG_MAX 998244353 998244353 998244353 998244353 = 119 × 2 23 + 1 998244353 = 119 \times 2^{23} + 1 998244353 = 119 × 2 23 + 1 φ ( 998244353 ) = 998244352 = 119 × 2 23 \varphi(998244353) = 998244352 = 119 \times 2 ^ {23} φ ( 998244353 ) = 998244352 = 119 × 2 23 因为 ω n = g φ ( m ) / n \omega_n = g ^ {\varphi(m) / n} ω n = g φ ( m ) / n 998244353 998244353 998244353 n n n 2 23 = 8388608 ≈ 8 e 6 2 ^ {23} = 8388608 \approx 8e6 2 23 = 8388608 ≈ 8 e 6
它的最小的原根为 3 3 3
代码实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void NTT (int T, vector<int > &A, int type) for (int i = 0 ; i < T; i ++) R[i] = (R[i >> 1 ] >> 1 ) | (i & 1 ? T >> 1 : 0 ); for (int i = 0 ; i < T; i ++) if (i < R[i]) swap (A[i], A[R[i]]); for (int cur = 1 ; cur < T; cur <<= 1 ) { int base = ksm (type == 1 ? ord : invord, (mod - 1 ) / (cur << 1 )); static int comp[N]; for (int i = comp[0 ] = 1 ; i < cur; i ++) comp[i] = comp[i - 1 ] * base % mod; for (int L = 0 ; L < T; L += cur << 1 ) { for (int j = 0 ; j < cur; j ++) { int tempx = A[L | j], tempy = comp[j] * A[L | j | cur] % mod; A[L | j] = (tempx + tempy) % mod, A[L | j | cur] = (tempx - tempy + mod) % mod; } } } if (type == 1 ) return ; for (int i = 0 , inv = ksm (T, mod - 2 ); i < T; i ++) A[i] * inv % mod; }
Reference
复数 (数学) - 维基百科,自由的百科全书
棣莫弗公式 - 维基百科,自由的百科全书
多项式 - 维基百科,自由的百科全书
范德蒙矩阵 - 维基百科,自由的百科全书
多项式 I:拉格朗日插值与快速傅里叶变换 - qAlex_Weiq - 博客园
快速数论变换(NTT)小结 - 自为风月马前卒 - 博客园
原根 - OI Wiki
多项式与生成函数简介 - OI Wiki
快速傅里叶变换(FFT)——有史以来最巧妙的算法?_哔哩哔哩_bilibili
P4781 【模板】拉格朗日插值 - 洛谷
P3803 【模板】多项式乘法(FFT) - 洛谷
ChatGPT